Irregular Webcomic! #1420

Maxwell's equations are a set of four equations that describe the relations between electricity and magnetism. Written more neatly, they look like this:

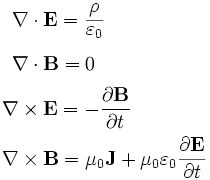
To understand the mathematical notation here, you need to know vector calculus. I believe, however, that anyone can understand Maxwell's equations, and why they are so important and amazing, if they're explained clearly enough.

Ready?

James Clerk Maxwell was a Scottish physicist who lived in the mid-19th century. He became interested in the then-fairly-new sciences of electricity and magnetism, and the intriguing hints that the two were somehow related to one another - hints that arose through the work of earlier scientists such as Hans Christian Ørsted, Michael Faraday and André-Marie Ampère. Ørsted had noticed in 1820 that the magnetic needle of a compass jumped away from pointing towards north when a nearby electric circuit supplied by a battery was switched on or off. This observation came as a complete surprise; up until then nobody had suspected that electricity had anything to do with magnetism.

Ampère soon heard of Ørsted's discovery, and within a week had formulated a mathematical theory to describe it. He posited that an electric current could generate a magnetic field, and that turning the current on or off meant that the magnetic field changed (from not being there to being there, or vice versa). This change in the magnetic field affected the compass needle. Faraday, meanwhile, worked on the opposite idea: that a changing magnetic field might cause an electric current to flow in a wire. He proved his theory and used it to invent the electric dynamo, an electricity generator essentially similar to the ones used today in electrical power stations. See, this stuff is important, and we haven't even reached Maxwell yet!

Maxwell formalised and extended the work of Ampère and Faraday, combining their discoveries into an interlinked set of equations that described fully every aspect of electricity and magnetism as they were then understood. Maxwell's equations still form the basis of electromagnetic theory as learnt by generations of physics students, and underpin everything we know about electromagnetism and do with it.

Equation One

The first equation says, in words, "the divergence of the electric field equals charge density divided by ε_o." Okay, so what does that mean? The ε_o (that's the Greek letter epsilon and a tiny zero subscript) is just a number; we'll get to that in a minute. Electric field is, in broad terms, a measure of how much electrical influence there is somewhere. If you've ever been to a science museum and stuck your hand on one of those electrostatic generators which make your hair stand on end, you know what an electric field feels like. (I'm deliberately simplifying and not using precise scientific definitions here, so people who understand formal electromagnetic theory, cut me some slack in my descriptions, okay? Thanks.)

Divergence is a mathematical measure of how much stuff comes from somewhere. For example: when you turn on a tap, water comes out. Mathematically, the divergence of water at the tap opening is a positive number. The divergence of water at the plughole in the sink where it vanishes is a negative number. Furthermore, as long as you're not taking water out of the system by filling a glass or something, the divergence of the whole shebang (tap plus plughole) adds up to zero, which means that you're removing exactly as much water with the plughole as you're adding from the tap.

So, the divergence (that's the triangle and the dot in the equation) of the electric field (the letter E) is how much electric field is coming from somewhere. This is equal to the electric charge density (the Greek symbol ρ, "rho") at the same place, divided by that ε_o number. Okay, now we know what the equation says, but what does it actually mean?

The amount of electric field coming from a region of space is equal to the total electric charge in that region of space, (divided by a number).

Electric charge is a property of subatomic particles, such as electrons and protons. Electrons have a negative charge, while protons have a positive charge. If a region of space has more protons than electrons, the total charge is positive, and the electric field coming from that region is positive. Protons are like taps for electric field. Electrons, on the other hand, are like sink plugholes for electric field. If a region of space has more electrons than protons, the total charge is negative, and the electric field coming from the region is negative - in other words the electric field goes into that region rather than "coming out" of it.

* Science is full of clever analogies. The most fun ones are where you compare something (say electric field) to something else (say, a flow of water), except for the fact that some major property of the something else (that the water moves) simply isn't there. Another example: Using a cellular phone is like speaking through a string so someone far away can hear you, but without the string.
** Yes, volts per metre. If you take two wires, one grounded and the other at 100 volts, and stick them a metre apart, you are generating an electric field of 100 volts per metre between them.
You can indeed think of the electric field as a flow of water, except that nothing actually moves*. However, if you stick an electric charge, say a proton, into an electric field, it will be carried along by the field, away from the tap and towards the plughole - i.e. away from areas of positive charge and towards regions of negative charge. An electron, being a negative charge, is carried in the opposite direction, away from the plughole (negative charge) and towards the tap (positive charge). This explains something you may have learnt in high school science classes: why things with the same electric charge are repelled from each other, while things of opposite electric charge are attracted to one another.

Pretty cool, huh?

Now, what about that dangling ε_o? This number is called the permittivity of free space. It is a constant, but its value depends on what units you use to describe electric charge and electric field. (If that seems odd, think of a car driving at a constant speed. The speed is constant, but it can be 50 miles per hour, or 80 kilometres per hour, depending on what units you use to measure it.) Physicists usually measure electric charge in units called coulombs, and electric field in units called volts per metre**.

Anyway, in those units, ε_o turns out to be approximately 0.0000000000088541878176. Remember that number.

Equation Two

Maxwell's second equation is a doddle now. The only new thing you need to know is that the letter B represents the magnetic field. Why B and not M? Heck if I know, but that's what it is. Anyway, knowing that, you can now read this equation yourself. The triangle and dot says "divergence" like in equation one. So the equation reads: "the divergence of the magnetic field is zero". Easy!

Ah, I hear you ask, but what does that actually mean?

It means that for magnetic fields, there are no things that act as taps or plugholes. Magnetic field doesn't come from anywhere or go away anywhere. But it certainly exists. How is this possible?

Magnetic fields "flow" from magnetic north poles to magnetic south poles (in the way that electric fields "flow" from protons to electrons - nothing actually moves.) But magnets always come with both a north pole and a south pole. If you cut a bar magnet in half, you don't get just a north pole and a separate south pole, you create two smaller magnets, each one with a north and south pole.

Magnetic fields don't come from north poles and go away at south poles. What happens is the magnetic field comes out of the magnet at the north pole, flows through space to the south pole, goes back into the magnet, and flows through the inside of the magnet back to the north pole, where it comes back out again. Magnetic fields go around in loops, never beginning, never ending. This is why if you cut a magnet in half you don't end up with single separate north and south poles. The half containing the original north pole still has a north pole at the same spot, where the magnetic field comes out, but the magnetic field has to go back into the magnet at the other end, and where the magnetic field goes into the magnet is a south pole!

In other words, single magnetic poles - or magnetic monopoles - do not exist. A magnetic monopole would be the magnetic equivalent of an electron or proton - a particle where magnetic fields emerge, or vanish from space.

Now, there's actually no strong theoretical reason why magnetic monopoles shouldn't exist. They just don't seem to. We've never seen one, despite many scientists looking for a long time. If they do turn out to exist, it's no disaster. All we need to do is add a "magnetic charge density" to Maxwell's second equation, in place of the zero, analogous to the electric charge density of equation one. Magnetic monopoles are thus good candidates for "exotic particles" in hard science fiction stories. You could probably do some cool things with them, if you could just find one.

Equation Three

On to equation three, which states that "curl of the electric field is minus the rate of change of the magnetic field". On the left side, E is our old friend the electric field. The triangle and cross represent the mathematical operation known as "curl", which is pretty much what is sounds like. The curl of the electric field is a measure of how "curly" it is, how much it twirls around in circles.

In terms of our water flowing analogy, if you look at a river, most of the water has no curl, as it's flowing straight along the riverbed. In some spots, however, the water swirls around in little eddies and whirlpools. At these spots, the curl of the water flow is non-zero. You can measure the curl of flowing water by sticking a tiny paddlewheel in it. If it spins around, the curl is non-zero; if it doesn't, the curl is zero.

The curl of the electric field is equal to... minus the rate of change of magnetic field. (The ∂ symbols and the t on the bottom are the mathematical symbols meaning "rate of change".) Rate of change is exactly what it sounds like: how fast the magnetic field is changing. If the magnetic field isn't changing, then the rate of change is zero, and the electric field is non-curly. If the magnetic field is changing, then the electric field goes curly. If the magnetic field is getting weaker, the rate of change is negative, and the electric field curliness is positive. If the magnetic field is getting stronger, the rate of change is positive, and the electric field curliness is negative - this just means that it rotates in the opposite direction.

How does a magnetic field get stronger or weaker? Well, we're talking about the magnetic field at some point in space. If the magnetic field there is zero, and we bring a magnet close, the magnetic field gets stronger. If we take it away, it gets weaker. Basically, if we wiggle magnets around, we generate changing magnetic fields. Changing magnetic fields generate curliness in the electric field. But what does a curly electric field mean?

Curliness in the electric field pushes electric charges around in circles.

Pause there for a second.

Electric charges going around in circles is an electric current.

Join the dots...

Wiggling. Magnets. Around. Generates. Electric. Currents.

This is the basis of Faraday's breakthrough invention: the electric generator. He realised that if you got some wires, and wiggled some magnets around near them, you would generate electricity. If you get something, say a steam engine, or a water wheel, to wiggle the magnets for you, you have a modern day coal-fired or hydroelectric power station. Without James Clerk Maxwell, his predecessors, and his equations, our lives would be very, very different. I hope you're starting to understand just how important these equations are (if you didn't already know).

And we still have one equation to go.

Equation Four

By now you should be able to read almost all of equation four by yourself. "The curl of the magnetic field equals μ_o times the letter J, plus μ_o times ε_o times the rate of change of electric field." Correct! The new term J refers to current density, which I'll explain in a minute. This equation is a bit of a mouthful, so let's take it one bit at a time.

In fact, let's start with the curl of the magnetic field. How curly is a magnetic field? Well, we've already seen that magnetic field always goes around in loops, from north pole, to south pole, and then back to north pole inside the magnet. Yes, that means it's always curly. The stronger the magnetic field, the tighter the loops are - and the more curly it is. In fact, the curliness of a magnetic field is basically a measure of how strong it is.

So the curliness (or strength) of a magnetic field is equal to μ_o times current density (plus the other bit, which we'll get to in a moment). Current density is how much electric current is present somewhere. What this part of the equation says is that if you have an electric current, there is always a magnetic field curling around it.

*** What happens when you switch an appliance on? You suddenly go from no electric current to some electric current. That means before there was no magnetic field, and suddenly you are generating a magnetic field. The magnetic field is getting stronger. Remember equation three? A changing magnetic field generates an electric current... This is the source of potential interference between your electrical appliances. This is why operating your blender makes your TV go fuzzy. This is why your computer cables are shielded, to prevent all the changing magnetic fields in your house from futzing with your precious data.
Imagine a wire carrying electric current. Wrap your fist around the wire, curling your fingers around it. Your fingers are curling in the same way as magnetic field is curling in circles around the wire. This is how electromagnets work. They have lots of wires, and when electric current passes through them, they generate a magnetic field. All the active wires in your house are generating magnetic fields too, though relatively weak ones.***

Again, like ε_o, the μ_o (Greek letter mu and a subscript zero) term is just a constant number that makes the units of measurement come out right. It's called the permeability of free space. When the magnetic field is measured in teslas and current density in amperes per square metre, μ_o equals about 0.000001256637061. Again, remember that number.

Notice that this equation is to magnetic field what equation one is to electric field. Equation one says that the amount of electric field depends on the amount of electric charge. Equation four says that the amount of magnetic field depends on the amount of electric current. Curiouser and curiouser...

Now, what about that last extra term: "μ_o times ε_o times the rate of change of electric field"? By now, this shouldn't be too hard to understand. If there's an electric field that gets stronger or weaker, it generates magnetic field. That was easy!

That last bit was Maxwell's major achievement, his crowning glory, his enduring and profound addition to our understanding of the universe. What it says is that to generate a magnetic field, you don't even need to have any electric current at all. All you need is a changing electric field.

I hope you'll excuse me if I guide you by the hand through the implications of this.

If you have a changing electric field, you will generate a magnetic field. Imagine you have an electric field that oscillates, wobbling back and forth from positive to negative. That will generate a magnetic field. What's more, because the electric field's rate of change has to change in order to allow it to wobble back and forth, the magnetic field will not be constant, it will change over time.

But remember what equation three told us: if you have a changing magnetic field, you generate an electric field.

The wobbling magnetic field will generate a wobbling electric field. That wobbling electric field generates a wobbling magnetic field. That wobbling magnetic field generates a wobbling electric field...

You can do some mathematics with equations three and four if you assume the current density J is zero (i.e. there are no electric currents). I won't go into the algebra, but they turn into the following:

As you can see, these are completely identical, except that one refers only to electric field, while the other refers only to magnetic field. In essence, what these two equations say is that an electric field that changes in time (on the right) generates an electric field that changes in space (on the left) in a precisely determined way, and likewise for magnetic field. In fact, these equations describe the motion of ripples of electric and magnetic field, which travel through space like waves.

If you know much about differential equations, you can solve these equations to work out the speed at which these waves travel. The speed works out to depend on those numbers ε_o and μ_o. The speed is:

Imagine you are James Clerk Maxwell, in 1865, formulating your theory of electricity and magnetism, and writing down your four equations for the first time in history. You write down the terms of these equations based on your experiments with electric batteries, bits of wire, and magnets. You realise you need to define some constants (ε_o and μ_o) to make the numbers come out right. You can measure the values of those constants using your batteries and wires and magnets, and you do so. The numbers don't make any sense to you at the time - they're just some sort of constants that nature seems to use. They could be any values at all, as far as you know or care. Anyway, you measure the numbers and you write them down.

You notice that if you apply some algebra to your new equations, you can generate an equation that only refers to the electric field, and an almost identical equation that refers to the magnetic field. You solve them and realise that these equations describe the motions of waves of electric and magnetic fields. You do the algebra to calculate the speed of the waves and realise it depends on those values you measured for ε_o and μ_o.

So you do the arithmetic. You take the values you measured for ε_o and μ_o, multiply them together, take the square root, and then take the reciprocal. The answer is a speed, so it has units of speed, in this case metres per second. And the answer is very close to 300,000,000 metres per second. Converted into miles, that's a tad over 186,000 miles per second. Being James Clerk Maxwell, and a brilliant physicist, you immediately recognise what this number is.

The speed of light.

Where the heck did that come from??

You, James Clerk Maxwell, know in 1865 from the work of Isaac Newton and others that light has certain properties: that white light is composed of multiple colours of light mixed together; that transparent materials such as glass bends rays of light and can be used to focus them into images, such as in telescopes; and that light diffracts through small holes and around sharp edges. This diffraction property can only be explained by supposing that light is made of some sort of waves. But nobody in the world knows what sort of waves they are. Nobody knows what light actually is.

You stop.

Nobody in the world - except you - knows what light actually is.

When you were writing down your equations, you were thinking about electricity and magnetism. Light was the farthest thing from your mind. You had not the slightest clue (and nor did anyone else) that light was related to electricity or magnetism. But there it is, falling out of your equations.

You realise that you are the first person in all of history to know what light is made of. Can you imagine that feeling?

Maxwell's equations gave humanity, finally, an understanding of what light actually is. His discovery was stunning and revolutionary. Light is electric and magnetic fields, wriggling through space together.

From this breakthrough have come countless other discoveries about the nature of light, as well as its sibling electromagnetic waves: radio, microwaves, infrared and ultraviolet, x-rays, and gamma rays. All these forms of radiation are made of electric and magnetic fields, moving through space at the speed of light, exactly as described by Maxwell's equations. We now know that radio waves, for example, can be generated by switching an electric current on and off at high speed. The electrons in the wires wiggle back and forth, creating wiggling electric fields, which create magnetic fields, and so on - the overall effect being radio waves. And radio waves in turn wiggle the electrons in your radio or TV antenna, creating electric currents that various electric circuits turn back into sound and pictures. I could go on with example after example.

Vast quantities of the technology we use every day makes intimate use of our knowledge of electromagnetism and its interaction with light. Civilisation as we know it would simply not exist without James Clerk Maxwell and his four equations. I hope I've managed to give you some insight into how wonderful they truly are.

2016-07-27 Rerun commentary: Well, there's not much more I can really add to this in the reruns.

Something I can say is that this has been one of the most popular comic annotations that I have written. It's linked from around 200 different sites on the web, and has generated more complimentary email than almost any other strip I've done. (I don't keep an exact count of how many emails I receive for each strip, so it's possible there are one or two other more popular ones. But this one is certainly in the top few.)

Which is very pleasing!

Sometimes it's difficult for me to know whether people like my stuff more for the comic gags and story, or for the occasional informative annotations. I don't think there's any doubt with this one. In all the correspondence I've received about it, I don't think anyone has complimented the joke in the comic. :-)

ADDITIONAL NOTE: A reader has pointed out a very specific inaccuracy in my descriptions of electric and magnetic fields above. As I stated, my wording was a little bit simplified and imprecise, but I think it's worth mentioning this specific inaccuracy just to set the record straight.

When I talked about "electric fields" and "magnetic fields", my language sometimes (but not always) implied that these were separate, localised things, and that there could be multiple electric fields or magnetic fields.

More accurately, there really is only one electric field, and one magnetic field - each one filling the entirety of the universe. The electric field is really just the sum total of the electric field strength and direction measured at every point in space (and similarly for the magnetic field). When I talk about a wiggling magnet "generating an electric field", what I really mean is that a wiggling magnet causes the strength of the electric field nearby to change.

And for the propagation of light, when I say "Light is electric and magnetic fields, wriggling through space together", what I really mean is "Light is disturbances in the electric field and the magnetic field, wriggling through space together".

If you take this into consideration when reading the above explanations of Maxwell's equations, you'll have a slightly more accurate picture of how electromagnetism works.