

| Archive Blog Cast Forum RSS Books! Poll Results About Search Fan Art Podcast More Stuff Random |
|
Classic comic reruns every day
|
1 Lambert: My great uncle Hillbert owned a hotel, burrowed out of a hill. Any time an extra guest showed up, he’d tunnel a new room to fit them in.
2 Lambert: Before long he had an infinite number of rooms.
3 Lambert: He hired some especially clever housing dwarves to do the construction. Each room was half the size of the one before.
4 Alvissa: That sounds very unusual.
4 Lambert: Oh, no, a compact house-dwarf space is definitely normal.
|
First (1) | Previous (4336) | Next (4338) || Latest Rerun (2895) |
Latest New (5380) First 5 | Previous 5 | Next 5 | Latest 5 Fantasy theme: First | Previous | Next | Latest || First 5 | Previous 5 | Next 5 | Latest 5 This strip's permanent URL: http://www.irregularwebcomic.net/4337.html
Annotations off: turn on
Annotations on: turn off
|
The German mathematician David Hilbert came up with the idea of the Grand Hotel, a hotel with an infinite number of rooms, which could be used to illustrate some seemingly paradoxical results in mathematics.
Before looking at those results, we need to specify exactly what infinity of rooms the Grand Hotel has. Recall from comic #3727 that there are different types of infinities, and that they can sensibly be said to have different sizes. The first and smallest infinite number is the number of natural numbers (or counting numbers: 0, 1, 2, 3, ...), which is said to be countably infinite, and which is represented by the symbol ℵ0.
Hilbert's Grand Hotel has ℵ0 rooms. You can think of them as being numbered, using the natural numbers: 0, 1, 2, 3, ... There are an infinite number of rooms because whatever room number you think of, there are more rooms with higher numbers. Since hotels don't normally have a room 0, we'll remove that one from the numbering scheme and assume our hotel rooms are numbered beginning from 1. (This doesn't change the fact that there are a countably infinite number of rooms, and also makes the following discussion a bit easier.)
The interesting part about this hotel happens when you consider what happens when every room is occupied. Now, if a normal hotel is full, and a new guest shows up, that's tough luck. There's nowhere to put the extra guest, and they have to go find a different hotel.
Not so at Hilbert's Grand Hotel! If the hotel is fully occupied (i.e. every room has an occupant), and a new guest arrives, Hilbert can simply reassign the room numbers as follows: The guest in room 1 moves to room 2, the guest in room 2 moves to room 3, the guest in room 3 moves to room 4, ... the guest in room n moves to room n + 1, ...
When this moving is done (all guests move at the same time, so the moves can be completed in a finite amount of time - probably just a few minutes), every guest still has a room, and room 1 is now empty! The new guest can be comfortably accommodated in room 1.
But that's not all. Imagine that a whole coach full of new guests arrive, let's say 100 more guests. In this case, if the hotel is fully occupied, then reassign room numbers thus: The guest in room 1 moves to room 101, the guest in room 2 moves to room 102, the guest in room 3 moves to room 103, ... the guest in room n moves to room n+100, ...
Then rooms 1-100 will be free, and all 100 of the new guests can move into an empty room. Similarly, if the hotel is full and any finite number G of new guests arrive, you can give all of them a room by moving each existing guest from room n to room n + G, this freeing up the first G rooms.
But wait, there's more. Imagine a coach arrives containing an infinite number of new guests. To be specific, a countably infinite number ℵ0 of new guests - which we can picture by imagining that every seat on the coach is numbered from 1, 2, 3, ..., so that each passenger has a number p. What is Hilbert to do now? He can't move each guest to their current room number plus ℵ0, because n + ℵ0 is not a natural number, and so there are no rooms numbered like that.
What he can do instead is reassign the room numbers as follows: The guest in room 1 moves to room 2, the guest in room 2 moves to room 4, the guest in room 3 moves to room 6, ... the guest in room n moves to room 2n, ...
Now all of the even numbered rooms (ℵ0 of them) are occupied, but all the odd numbered rooms (ℵ0 of them) are vacant! The infinite number of new guests can comfortably move into the odd numbered rooms, one guest per room. Specifically, you could assign coach passenger p to room 2p - 1.
But wait... Imagine not one coach with an infinite number of passengers arrives, but an infinite number of such coaches arrive at once! Again, we'll consider the case where the number of coaches is countably infinite, ℵ0, so each coach can have a unique natural number c assigned to it.
The canny Hilbert now reassigns each guest currently in room n to the new room (n2 + n)/2, and gives each passenger number p from coach c the key to room [(c + p - 1)2 + c + p - 1]/2 + p. While it may not be obvious, this assignment houses each existing guest, plus all of the infinite number of new guests from each of the infinite number of coaches to a unique room, so they can all be accommodated comfortably, one person per room. (There are also several other schemes that Hilbert could use to do this.)
All of this is really just a way of demonstrating that all countably infinite sets of things are the same size. You can add a few more to the set, you can double the set, you can add a (countably) infinite number of copies of the set to itself, and you always end up with the same number. More concretely:
Okay. At this point we've explained up to panel 2 of the comic.
How do you fit an infinite number of rooms into a hotel, or in Uncle Hillbert's case, a hill, where we wish to assume the total volume of the hotel/hill is finite? For this trick we need the concept of infinite series. An infinite series is a sum of numerical terms, that goes on forever. An example is 1 + 2 + 3 + 4 + ...
In this example, the total obviously gets bigger with every term that is added. So the total gets bigger without limit - meaning that for any number N we care to name, we can find some number n such that we can add up the first n terms of the series to exceed N (and then adding more terms will just make it even bigger).
But there are other infinite series which don't get bigger without limit. Consider this one:
1 + 1/2 + 1/4 + 1/8 + 1/16 + ...
If we look at the progressive sum after each term, it goes like this:
1, 1 1/2, 1 3/4, 1 7/8, 1 15/16, ...
You can probably see that at each step we're going exactly half of the rest of the way towards a total of 2, but that we will never actually reach 2, no matter how many more terms we add. If we could somehow add together an infinite number of terms, we might reasonably expect that the total would actually be 2. There are some mathematical formalities to be taken care of, but this is more or less correct. So it's possible to have an infinite number of numbers added up, to produce a finite total. In this way, by making each hotel room half the size of the one before, it's possible to fit all of the infinite number of rooms into a finite sized hotel (or hill).
Right. Three panels of the comic down, one to go. Okay, strap yourselves in...
For this one we have to venture into the field of mathematics known as topology. Before I got to university and studied it formally, I always thought of topology as a fun area of mathematics. Topology is related to such cool and interesting things as the Seven Bridges of Königsberg, Möbius strips, mazes, and disentanglement puzzles, not to mention the cool idea that a coffee cup is somehow "topologically" the same as a doughnut, because (if they were made of suitably pliable material) you can stretch one shape into the other without tearing any holes in it.
Topology deals with geometric problems that do not depend on the exact shape of objects, but only on the "connectedness" of objects. For example, in the above-mentioned Seven Bridges of Königsberg problem, the original problem asked if it was possible to devise a walking path that would cross all seven bridges in the city exactly once each. In 1736 Leonhard Euler proved that such a path was impossible. To tackle the problem, he pointed out that the lengths of the bridges and the distances between them were irrelevant - the only relevant detail was which end of which bridge you could reach by walking from specific ends of the other bridges (restricted by the rivers which the bridges cross).
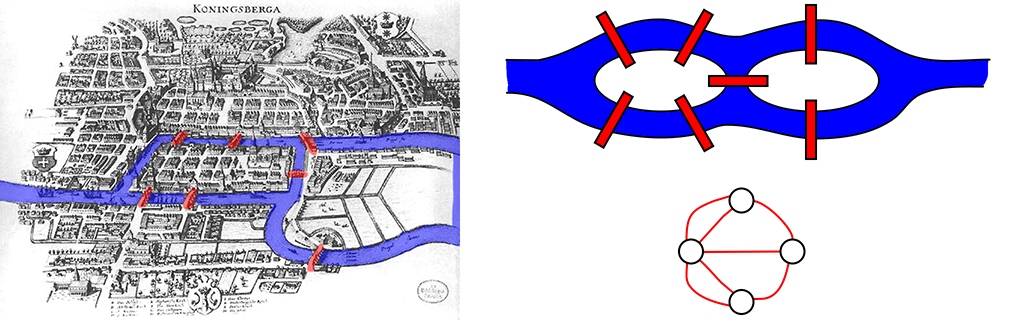
The diagram above shows a historical map of Königsberg on the left, showing the seven bridges (red). The island on the right is very large, but shown with a blue edge on the right to make it clear that it's an island. The diagram on the upper right is a simplified diagram that abstracts the geographical shapes and distances, but preserves the relationships between the bridges and islands. On the lower right is a graph, with the upper and lower nodes representing the river banks, the left and right nodes the islands, and the red connecting edges represent the bridges. Solving the problem of trying to traverse each bridge/edge exactly once is equivalent in all three representations.
Formalising this rather elusive geometrical property into a mathematical framework took some time. Incremental contributions by many mathematicians over the following centuries ultimately led to the first mathematically rigorous definitions of topological properties in the early 20th century. It turns out that capturing the essential properties of topological objects without adding a bunch of unnecessary stuff is a little tricky, so the definition is not entirely intuitive. For beginners, in a topological object there is no way of measuring distance - no way to tell how far apart two points are. We're used to being able to measure distances between things, but to capture the essence of topology you have to throw this away and consider objects that can't be measured.
To begin, we go back to the thing that underlies virtually all of mathematics: sets. A set is just a collection of objects. Each object in a set has to be different - you can't have two copies of the same object. And that's it. You can have a set of numbers, for example {1, 2, 3}. However, numbers come with unnecessary baggage. People seeing the numbers 1 and 2 might conclude that they are "closer together" than the numbers 1 and 3. But for the purposes of a set, there is no concept of distance - it doesn't even make sense to talk about two objects in a set being "closer together" than another pair of objects in the set. (You can decide to build a set with additional properties that allow such measurement, but it's not intrinsic to the definition of a set.)
Also, there is no ordering in a set. To write a set down in writing, we need to list the elements in some order, but the ordering we choose to write down is not a property of the set. The set {1, 2, 3} is the same as the set {3, 2, 1}. (Again, you can decide to build a set with additional properties that allow such ordering, but it's not intrinsic to the definition of a set.)
To get around this mental baggage with numbers, we can consider sets of other objects that have no natural distance or ordering, such as {🔴, 🔵, 🟠}, or {▲, ☐, ●}. These are just as valid as mathematical sets.
To turn a set into a topological space, we need to add an additional property related to measurement, although not fully-fledged measurement that you get with things like numbers. Specifically, all that we need is a concept of neighbourhoods of members. You can think of a neighbourhood of a given member ▲ as a collection of members of the set that are all "close" to ▲ in some sense - although within any given neighbourhood it is not necessarily possible to say which members of the neighbourhood are closer or further apart. A neighbourhood of ▲, in other words, is just a set—a collection of objects—made up of some of the members of the main set. In mathematical terms, this is a subset of the main set.
To define a topology on our set, we need a bunch of neighbourhoods, or subsets, that obey some particular properties. These properties are:
These definitions are due to the German mathematician Felix Hausdorff, who features in the next part of our story. With these definitions of a topological space, you can start to do some cool mathematics on geometrical shapes - mathematics that doesn't rely on any measure of distance.
An example of a topological space is all of the points on a line. The neighbourhoods of each point P on the line can be defined as every open interval that contains P. By an open interval, we mean start at P and move along the line in one direction by any non-zero distance to another point Q, and then start at P and move along the line in the opposite direction by any (possibly different) non-zero distance to a third point R. The open interval is every point between Q and R, not including points Q and R themselves (this is important, and the bit that makes the interval "open"). Every such open interval containing P is a neighbourhood of P. Also, the whole line is a neighbourhood of P. If you're keen, you can go through the above four properties of neighbourhoods and convince yourself that they are all true.
Another example of a topological space is all the points on a circle (the boundary, not the interior). The neighbourhoods of any point P on the circle are defined similarly, by moving outwards in different directions to points Q and R and considering the open interval between Q and R to be a neighbourhood. Also the whole circle is a neighbourhood of P. Similarly, you can define the points on the boundary of a square, or a triangle to be a topological space.
You can also define the surface of a sphere to be a topological space. In this case, to define a neighbourhood of a point P, draw any line that connects up such that it divides the surface of the sphere into two pieces, one piece containing P and the other not containing P. Then the set of points in the piece containing P, not including the points on the dividing line itself (i.e. the open set), is a neighbourhood of P. Also, the whole sphere is a neighbourhood of P. Similarly you can define the surfaces of ellipsoids, cubes, pyramids, etc., as topological spaces.
Now let's consider a torus, or a doughnut shape, a solid with a hole through it. You can define a topology on the surface of a torus in a similar way to that on a sphere above, however you need to be careful. Some neighbourhoods can be drawn with a single line, like on the sphere (left image in the diagram below). But if the line goes through or around the hole, then the line won't divide the surface into two separate pieces - you need to draw a second line to divide the surface, and thus define your neighbourhoods (right image in the diagram below). As with the sphere, the points on the dividing lines (the black lines in the diagrams) are not included in the neighbourhoods (the neighbourhoods are open).
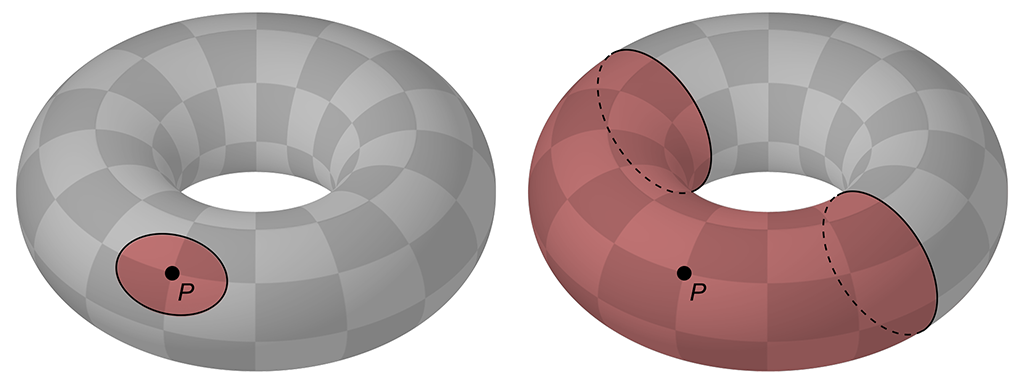
Now the interesting thing with these definitions is that you can now demonstrate that a straight line is topologically different to a circle, whereas a circle is topologically indistinguishable from a square or a triangle - because of the difference in the connectivity of the neighbourhoods. And similarly, you can show that a sphere, ellipsoid, cube, pyramid are all topologically equivalent, whereas a torus is topologically different, because of the hole in it that requires you to change how the neighbourhoods are defined. Drawing neighbourhoods on the surface of a coffee cup results in the same need to be careful around the hole in the handle as the hole in the torus, but no other complications. And so you can show that a coffee cup is topologically equivalent to a torus.
Okay, that was a kind of diversion to show how this definition of topology can be useful and interesting. Let's get back to Herr Hausdorff. When Hausdorff came up with the definitions of neighbourhoods in a topological space listed above, he also included another requirement, which was later shown not to be necessary in general. It was this:
In other words, for any two points, there are neighbourhoods of those points that don't overlap. A topological space that additionally satisfies this condition is known as a Hausdorff space. As my topology lecturer said when teaching us this concept, in a Hausdorff space, all the points are "haus-dorff" ("housed off") from one another.
Hausdorff included this condition because it seems so natural as a property of topological spaces. For points that are "far apart" (e.g. on the surface of a sphere) you can easily draw neighbourhoods around each one that don't overlap. As the points get "closer" together, the neighbourhoods just need to shrink. As long as the two points aren't the same point they have some "distance" between them and you can draw non-overlapping neighbourhoods. And if you're looking at a discrete set like {▲, ☐, ●}, you can just say that {▲} is a neighbourhood of ▲, and {☐} is a neighbourhood of ☐ and those neighbourhoods don't overlap.
In fact, Hausdorff-ness seems so intuitive that it's hard to think of examples of topological spaces that aren't Hausdorff. Indeed, every example of a non-Hausdorff topological space is somewhat pathological, and it's difficult to give an easily understandable example. The simplest one is called the cofinite topology. This is a topology on an infinite set where every neighbourhood is infinite, and the complement of every neighbourhood (i.e. the members of the set not in the neighbourhood) is finite: There is no neighbourhood {▲} of the set member ▲, because every neighbourhood of ▲ contains an infinite number of members of the set. I'll leave further consideration of this as an exercise for the reader.[1]
Okay, now we know what a Hausdorff space is. We're one third of the way through panel 4 of the comic. Grab a drink and settle in for the remaining two-thirds.
The next thing we can consider about a topological space is a property known as compactness. Before attempting to explain what compactness means (in the formal mathematical sense), I have to admit that I don't have a very good intuitive feel for what compactness is. It's been long enough since my university courses in topology that I didn't remember what it meant, and had to read up on it - and then I discovered that I couldn't really wrap my head fully around the concept any more. I figured there had to be some more intuitive way of thinking about compactness than the abstruse formal definitions offered in Wikipedia and other online resources, and so I went looking for them.
It seems I'm far from the only person to go in search of an intuitive understanding of compactness, because this question is asked many times on many different sites including StackExchange, MathOverflow, PhysicsForums, Quora, and Reddit. Perhaps the most revealing answer was this one that I found on Reddit:
[Compactness] seemed artificial to me at first too, but if you work with it enough for a semester, you'll learn to love it. It's just a very useful property that someone probably originally defined because they could see it'd be useful (not based off any crazy intuition).
— https://www.reddit.com/r/math/comments/1g90d1/what_is_the_intuition_behind_the_definition_of/
Since I don't have a whole semester to explain and get you to do exercises on it so that you understand the concept, I'll just have to go with an abstruse definition and make the most of it. To begin, we have to define the concept of a cover of a set. This is not too bad. A cover of a set is a collection of subsets such that the union of the subsets contains all the points in the original set. If you think of the set as the surface of a bed, think of a cover as a bunch of blankets, which together cover all parts of the bed.
Now we need the concept of an open cover. This is a cover in which each subset in the cover is an open set (as defined above - intuitively, a set that doesn't include its boundary points). In our bed analogy, points on the bed under the very edge of a blanket are not considered to be covered. Now:
In our blanket analogy: the bed is compact if for every different covering of blankets, you can pick a finite number of the blankets that still covers the bed. Here's where the analogy stretches a bit, because you really need to consider beds that have covers made of an infinite number of blankets.
Under this definition, any finite topological space (a set with a finite number of elements) is compact. So the distinction between compact and non-compact spaces is only important for topologies with an infinite number of points. Consider our first two examples of infinite topological spaces above: (A) all the points on a line, (B) all the points on a circle.
If we rope in some ideas about distance—remembering that any way of measuring distance is not necessarily present in the topologies, but which merely makes describing these examples a lot easier—then we can think about the straight line as being a number line. I can define an open cover of the line as consisting of all of the open intervals (n, n + 2), for each integer n (positive, negative, and 0). These intervals are all "length 2", but don't include their endpoints. So the interval (-1, 1) doesn't include -1 or 1, but the interval (0, 2) includes 1, so 1 is covered. Now, this collection of open intervals covers the line, but it is infinite. Furthermore, you can't remove any of the intervals - if you remove the interval (0, 2) then the point 1 will no longer be covered. So this cover of the line does not have a finite subset that also covers the line. So the straight line is not compact.
Now think about the circle. There are infinitely many points on the circle (since between any two different points there is another different point). You can cover them with open intervals in the same way as described above for the line. But because the circle turns back on itself, if all the open intervals are the same "length" then you only need a finite number of them. There are other examples where you can construct covers consisting of an infinite number of open sets of different "lengths", but it can be shown (I'm not going to prove it here) that for any such cover, you can always choose a finite subset of the cover that still covers the circle. So the circle is compact.
Compactness embodies some sense of the topological space "not extending out to infinity", although this doesn't quite encapsulate all of the qualities of compactness. The points on the surface of a sphere are compact. The points on the surface of an infinitely long cylinder are not compact. This is a rough intuitive idea of what compactness means, but as stated it's not a full understanding of all of the properties, and I'm sorry that I'm having difficulty getting all of that across here.[2]
Anyway, we're now 2/3 of the way through the last panel of the comic. We're on the home stretch now!
A normal space is a topological space that satisfies the following condition:
A closed set what you might expect: the opposite of an open set, or a set that includes the points on the boundary. If we take two closed sets A and B that are disjoint (i.e. they don't overlap; they have no members in common), then in a normal space each of these sets will have some neighbourhood such that the two neighbourhoods also don't overlap. A neighbourhood of a set is basically just a neighbourhood that is a neighbourhood of every member in the set.
In a sense, this is kind of the Hausdorff condition applied to (closed) sets of points rather than just two points. In a normal space, you can take any two clumps of points, and as long as the clumps don't overlap, you can draw neighbourhoods around each clump that don't overlap. So now we know what a normal space is.
And, putting it all together, there is a theorem in topology that says: A compact Hausdorff space is normal. I leave the proof of this theorem as an exercise for the reader.
Thus we have shown that the joke makes sense, and the comic has been formally proven to be funny.[3] Q.E.D.
[1] Mathematician Rob E. writes:
I must strenuously object to the statement that all non-Hausdorff topological spaces are "somewhat pathological". The Zariski topology, which in a one-dimensional space coincides with the cofinite topology mentioned above, is not at all pathological. It is the natural topology obtained by considering polynomials to be the continuous functions. This topology lies at the roots of algebraic geometry, which occupies a central place in modern mathematics (if you believe the claim on Wikipedia, which was probably* not at all written by an algebraic geometer).
* With some potentially nonzero probability.
[2] Mathematician Benjamin D. writes:
My own intuition for compactness is that it's a smallness condition, but a smallness condition that cares about continuous functions. Being a bit more precise, there are some properties that, say, finite sets have. If you have a function from a finite set into the reals (that is, if you pick out some finite subset of the reals), it has a minimum and a maximum, if you take an infinite sequence inside a finite set, it has some subsequence which is constant. Compactness is a condition that lets us extend this to continuous functions—a continuous function from a compact space into the reals has a minimum and a maximum, and any infinite sequence in a compact space has a convergent subsequence. We can think of these as kind of continuous versions of the properties for finite sets. (This is also how Terry Tao describes the ideas in his notes on compactness).
This, to me, justifies the weird definition—instead of working with an arbitrary collection of neighborhoods (which could be infinite, or uncountable, or have one neighborhood for every single element of the underlying set, which is probably huge), we can trim it down to working with finitely many. How many? Well, depends on the neighborhoods we started with, of course, but some finite number. Then, once we've brought this into the realm of finite numbers, we have a lot more room to mess around. The particular fact that becomes really useful in the case of the theorem you mention is that while the intersection of arbitrarily many open sets doesn't have to be open, the intersection of finitely many open sets is always open.
Something that might be useful for the intuition, too, is the fact that (in the real numbers, or in any Euclidean space) a set is compact if and only if it's closed and bounded. "Bounded" is precisely what you're getting at with the "not extending out to infinity," of course, but it turns out that if you add in the condition of being closed (which I always think of as containing all of its limit points), that's enough to guarantee that you're compact.
One direction of that, of course, isn't terrible. Any compact set in Euclidean space has to be closed and bounded (If you think it might be useful for your readers to have a quick write-up proving those facts, I'm more than happy to hack something out). The really remarkable and surprising fact (well, surprising to me) is that the converse holds too: any closed, bounded subset of Euclidean space is compact!
The definition of compactness is definitely not something that came to one person in a flash of brilliance! This was workshopped by many mathematicians over many years, it's as much a process as the modern models of an atom or the solar system. One paper discussing this is linked here.
Something that's very surprising, in some ways, is that this notion of compactness turns out to be very linked to all kinds of modern math—it shows up in set theory, in trying to find solutions to differential equations, and in many other places besides. It really is a very fundamental tool of math as we know it, and it's a pretty recent discovery—I'm not sure if there was any carefully formulated definition of compactness before the nineteenth century.
[3] An earlier version of the comic had the final line reading: "Oh, no, a compact house-dwarf space is completely normal." One of my friends pointed out that "completely normal" actually also has a formal mathematical definition, that being that if every subspace of a normal topological space is also a normal space, then that topological space is completely normal. Furthermore, being compact and Hausdorff is not a sufficient condition for a topological space to be completely normal. Therefore that version of the joke was not funny at all.
|
LEGO® is a registered trademark of the LEGO Group of companies,
which does not sponsor, authorise, or endorse this site. This material is presented in accordance with the LEGO® Fair Play Guidelines. |