1 {photo of a blacksmith working red hot iron in a forge}
1 Caption: Blacksmith Physics

Not that sort of red hot.

Hot objects glow. That is, they give off light. Fires produce light, allowing us to see at night. Metal objects heated in a fire start to glow too, as do heating elements in electric ovens and toasters - which are heated by electricity.

The hotter an object is, the brighter it glows. The colour changes as well. If you take a piece of iron and heat it in a forge, it first begins to glow a dull red colour. As the temperature of the iron increases, it glows more brightly and the colour shifts through bright red to orange and yellow, until eventually it becomes "white hot".

Blacksmiths and others who work with hot metals know that you can judge the temperature of the metal pretty accurately simply by observing the colour with which it glows. If it's this particular shade of orange, then it's this temperature. In other words, the colour of the glow is determined solely by the temperature, pretty much.

You can use this to determine the temperature of things other than metals too. Our sun is a very bright yellowish-white colour. If you compare it to metals heated to various temperatures, you would guess that the temperature of the sun is about 5800 kelvins. And you'd be right, that is the temperature of the external layer of the sun that is emitting the light, the photosphere. (Other regions of the sun, both inside and outside the photosphere are much, much hotter. The outer corona is transparent though, so we don't see it, and the inner regions are hidden by the photosphere.)

If you extend this with telescopes and sensitive spectrometers, you can also measure the temperatures of stars.

Wait. Stop right there for a second. You can measure the temperatures of stars. Just by collecting their light and comparing the colour to the colours that iron glows when it's heated up. Isn't science wonderful?

This sort of red hot. Erupting lava on Stromboli, Italy.

Anyway. Reddish stars are literally glowing "red hot" and are cooler than yellow, white, and blue stars^[1]. So the question arises, why do hot objects glow? And why does the colour depend on the temperature and not what the object is made of?

Lord Rayleigh (who we've met before, in the context of Rayleigh scattering and the colour of the sky) and James Jeans tackled this problem in the late 19th century. To do so, they assembled a detailed chain of argument and simplifying approximations, based on their knowledge of physics at the time. The arguments stem from the field of thermodynamics. As the name suggests, this is the study of the movement of heat. And heat, as we know from the work of James Joule in the mid-19th century, is a form of energy embodied by the kinetic energy (energy of motion) of the molecules in an object.

Heat energy can move around in three distinct ways:

1. Convection (mentioned briefly in this annotation on the Earth's interior). This is where hot objects physically move around, carrying their heat with them. It's usually seen in liquids and gases, as heat causes the material to circulate and mix. This is the movement of heat experienced when someone pees in the swimming pool.
2. Conduction. When a hot object is in direct contact with a cooler object, heat flows from the hot object into the cooler one. At the molecular level, this is because the molecules of the hot object have higher kinetic energy than the molecules of the cool object, and when they collide the energy tends to be equalised. The more energetic molecules slow down and the less energetic ones speed up until the energy distribution is pretty much even - which at the macroscopic level means the heat has flowed from hot to cool until the objects end up at the same temperature. This is the movement of heat experienced when you scald yourself by touching a hot object.

Hot chocolate circulates heat within itself by convection.

3. Radiation. The atoms in a hot object are vibrating, which means the electric charges in them are vibrating. From Maxwell's equations, we know that vibrating charges produce electromagnetic radiation, i.e. radio waves, microwaves, infrared radiation, light, ultraviolet, x-rays, or gamma rays. This thermal radiation (radiation produced by heat) carries energy away from the hot object, and when the radiation hits another object it can heat it up. This is the movement of heat experienced when the sun warms your exposed skin.

Now the problem of why hot things glow is a problem of heat radiation, not convection or conduction. So let's eliminate those two by considering a hot object that cannot convect or conduct heat to other objects. An object surrounded by a vacuum will do. The only way heat can escape is to be radiated away. We also need to consider what happens to incoming radiation. If our object is shiny or brightly coloured, it will reflect some of the incoming radiation. That's how we see objects - our eyes detect the light reflected off them. But reflected light isn't thermal radiation - it will confuse things. The reflected light off a shiny iron bar gets mixed up with the red-hot glow when it's heated. It might be a small contribution, but to simplify things, let's get rid of it by considering an object that doesn't reflect any light or radiation at all. Instead, it must absorb all of the incoming radiation that hits it. This absorption of energy will heat the object up, and the energy can be re-released as thermal radiation - that's okay, because it's part of the overall thermal radiation of the object.

Okay, we have our ideal test object. It absorbs every bit of radiation that hits it, and the only thing it radiates is thermally produced electromagnetic radiation. At low temperature, such an object will look completely black to our eyes. Blacker than any physical object you've ever seen - in fact, you can't see this object, it doesn't reflect any light at all. It would look like a featureless black blot, simply blocking out whatever is behind it. Such an idealised object is called a black body. Whatever radiation comes from a black body is purely thermal radiation, without any contamination from reflected light.

A real world approximation to a black body. (If this was spherical and frictionless, it would be more ideal.)

But when you heat up a black body to high enough temperatures, it starts to glow with thermal radiation in the visible part of the spectrum. First dull red, then brightly red-hot, then orange, yellow, to white-hot. A black body is only "black" to our eyes at low temperatures. But even at low temperatures it's emitting small amounts of thermal radiation in the infrared and radio parts of the spectrum - we just can't see it with our eyes.

For Rayleigh and Jeans, even this idealised black body object was still a bit too complicated to work with. They considered what sounds conceptually like a more complicated type of black body, but one which made the mathematics and physics easier to think about. Think of an oven or kiln. It's a big empty space at a high temperature. What Rayleigh and Jeans did was to think of this empty space as their black body. Not the oven around it - just the space inside the oven. If you make a small hole in the front of the oven, then you can see the black body. Any incoming radiation that falls on the black body—i.e. into the hole—vanishes into the empty space. In other words, it's completely absorbed - there's absolutely no chance of a reflection^[2]. The radiation that emerges from the hole is purely thermal radiation.

Now that we've set up this idealised black body, we can think about what sort of spectrum it has. The spectrum in this context is the distribution of energy along the continuum of wavelengths that make up the electromagnetic spectrum. What wavelengths carry the most energy? What wavelengths carry only a small fraction of it? The approach used by Rayleigh and Jeans was to consider how the waves can bounce around inside the cavity inside oven (i.e. in the "black body").

Large tiles and small tiles. To span the same distance without cutting, you have a limited selection of large tile sizes, but more choice of small tile sizes.

To start with, you need to assume some volume for the oven. Given that, you can calculate how many electromagnetic waves of any given wavelength can fit inside the oven. Think of it like a guitar string. The string is a specific length, determined by the position of the bridge at the bottom end and the fret near your finger. The string vibrates in a wave shape, similar to the vibration of the electric and magnetic fields in electromagnetic radiation. A guitar string vibrates at a specific frequency, because the wavelength is constrained to have fixed points (or nodes) at the ends. It can also vibrate at certain specific higher frequencies, where the wavelengths are smaller, but still constrained by the nodes at the ends^[3]. In a similar way, the size of the oven cavity determines a set of wavelengths that fit inside it. At long wavelengths, the constraint of fitting inside the oven is more severe, so only a few specific sizes fit in. At shorter wavelengths, many different wavelengths can fit into the given size.

Think of it like tiling a room, with the constraint that you're not allowed to cut the tiles. Let's say the room is 10 metres long. If you want to use large tiles, then you are constrained quite severely. You can use 1 metre tiles, and fit exactly 10 of them along the length of the room. If you would rather have 11 tiles, the tiles have to be 10/11 = 0.909 metres long (rounding off). You can't use tiles 0.95 metres long, or 0.97 metres long, or 0.9274 metres long. There's a huge gap in the allowable tile sizes. On the other hand, if you want to use small tiles, you could use 100 mm tiles and fit exactly 100 of them along the room. If you'd rather have 101 tiles, the tiles have to be 100/101 = 99.01 mm long. These tiles are almost the same size! For small tiles, the gap in allowable tile sizes is tiny, so you have a lot more choice of exactly what tile size you'd like to use. Similarly with our black body cavity: At long wavelengths, only a few different, widely spaced wavelengths are allowed. At short wavelengths, there are lots of different wavelengths that fit into the cavity.

The opening in this empanada oven is a very good approximation of the surface of a black body. The black body is the space inside the oven, not the oven itself.

Okay. The next step is realising that all of the waves in the cavity must be at the same temperature. In other words, if you convert their energy into thermal energy, it has to come out the same. So at long wavelengths, where there are fewer waves, there is less total energy. While at shorter wavelengths, there are many more available different wavelengths, and so more total energy. The same amount per wave (since they're at the same temperature), but more in total because there are more different waves. I'm skipping over the details of the maths, but if you actually do the calculation, you find that the volume of the oven cavity cancels out at this point, and you're left with a distribution of energy as a function of wavelength of the thermal radiation.

The resulting formula that Rayleigh and Jeans first thought of in 1900, and derived more rigorously in 1905, is called the Rayleigh-Jeans law. Here is the formula:

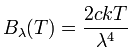
It says that the energy B radiated by a black body at a specific wavelength λ as a function of the temperature T is directly proportional to the temperature, and to 1/λ⁴. The two constants are c, the speed of light, and k, the Boltzmann constant. I haven't mentioned the Boltzmann constant before - it's the conversion factor between temperature T and kinetic energy (1/2 mv²) of the particles at that temperature (1/2 mv² = 3/2 kT), so you can probably see why it appears here. Notice that nothing here cares about what the object is made of. All that matters for thermal radiation is how hot the object is.

So now we know why a hot object emits radiation, and we have a theoretical model for exactly how much radiation it should emit and at what wavelengths. This applies to our hypothetical perfect black body. It doesn't work for reflective objects at cool temperatures - say a tennis ball at room temperature. Almost all of the light you see coming off a tennis ball is reflected sunlight (or room light, or whatever), not thermal radiation. But for objects that are very hot—hot enough to glow red-hot or brighter—most of the radiation they emit is thermal and we can mostly ignore the small amount of reflected light. So for many of the things where we are interested in thermal radiation, such as glowing hot iron, or stars, we can treat them as black bodies.

Treating hot objects as black bodies, we can now calculate what their spectrum looks like. A "red hot" object emits most of its thermal radiation around the red end of the visible spectrum. A hotter object emits more in the orange or yellow, and combines to give the object those distinctive colours. An even hotter object emits across the whole visible spectrum, and the combined light appears white to our eyes. Even hotter objects, such as the hottest stars, emit most of their visible thermal radiation in the blue end of the spectrum (but still quite a lot across the rest of the visible range), and the result is the faint bluish colour that some stars have. This colour range, and its strict relation to temperature, is called black-body radiation.

Lord Rayleigh (left) and James Jeans. Public domain images from Wikimedia Commons.

We've learnt quite a few things today. Firstly, this is a primer on black-body radiation, and the reason why things like stars are often referred to as "black bodies" even though they're glowing hot and bright. But beside that, there was the scientific process that Rayleigh and Jeans went through to understand thermal radiation. They simplified the problem so that they could tackle it with the physics they knew. They invented an idealised type of object, the black body, which removed some of the complications of real life objects. They proposed a strange example of what might make an ideal black body - the cavity inside an oven. They used this specific example to constrain their problem to a case that could be tackled mathematically. They did that maths, brought in knowledge gained by other people from related fields of study, and produced an answer. Then by comparing how the idealised case relates to the real world, they recognised in what cases their model might be useful to calculate results that can be applied to real world objects.

This is one of the processes of science. Many of the phenomena around us are incredibly complicated, involving interactions across many different physical processes. To understand, it helps to simplify down to a point where you can make calculations, then go back up the chain to the real world again and understand where your approximations are and when they are important.

---

I've skipped something important in this story. I've presented the work of Rayleigh and Jeans, and their resulting Rayleigh-Jeans law, as a triumph of reason over the physical world. There's a formula at the end of the process, and I then went on to describe how you can use this formula to understand the real world phenomena of glowing hot objects. It all sounds great.

Blacksmiths judge the temperature of hot iron by the colour it glows - using physics! Creative Commons Attribution-NonCommercial image by Flickr user ilker ender. This photo also appears as the title image for this annotation.

And this is partly true. The Rayleigh-Jeans law predicts the thermal radiation spectrum of hot objects really well. But only for some wavelengths. Specifically, it works for long wavelengths of electromagnetic radiation. Radio waves, microwaves, infrared radiation. The trouble is, the law predicts that the energy of thermal radiation varies as one over the fourth power of the wavelength. If the wavelength is really small, the energy should be really, really, really, really big. There should be heaps of ultraviolet radiation. Tons of x-rays. Enormous truckloads of gamma radiation. When we heat objects up, they should give off so much high-energy radiation that we would all be fried by x-rays and gamma rays.

Worse still, if you think of it purely mathematically, the amount of thermal radiation as you go to shorter and shorter wavelengths just keeps getting bigger and bigger, without limit. Every single object in the universe at a temperature higher than absolute zero should be emitting an infinite amount of energy, mostly in ultra-high energy gamma rays! Obviously (a) this isn't happening, so (b) something is wrong with the Rayleigh-Jeans law.

But the Rayleigh-Jeans law is based on our (1900-era) knowledge of physics, and it does work really well for long wavelengths - it gets those almost exactly right. So what's wrong with it?

Albert Michelson wrote in 1903 in his book Light waves and their uses:

The more important fundamental laws and facts of physical science have all been discovered, and these are so firmly established that the possibility of their ever being supplanted in consequence of new discoveries is exceedingly remote.

A more famous, but less well verified quotation comes from William Thomson, Lord Kelvin, purported to have said in a speech to the British Association for the Advancement of Science in 1900:

There is nothing new to be discovered in physics now. All that remains is more and more precise measurement.

This was the general feeling amongst scientists at the turn of the 19th to the 20th century. As a society we understood motion, atoms, energy, heat, electromagnetism, the nature of light. It was the first time we really felt comfortable in our understanding of everything about the universe. We knew how everything worked.

But there was this one little nagging problem with the spectrum of hot objects...

---

[1] The temperatures of stars can also be determined in other ways; I can think of at least two off the top of my head: (1) Measuring the broadening of spectral lines caused by the Doppler shift of thermal motion of gas in the star. (2) Modelling a star using known properties of gravity, gas, thermonuclear energy generation, and heat propagation. The cool thing is that all of these three methods give the same results. Science works, baby!

[2] The incoming radiation may potentially rattle around, reflecting inside the oven and potentially could emerge from the hole again, but we are really considering an idealised oven-like space, in which the walls absorb the radiation and convert it to heat before it has any real chance of emerging from the hole untouched.

[3] It's the specific combination of intensities of these different vibrations at specific higher frequencies (called harmonics) that give a guitar its distinctive sound - that makes it sound different to a piano string, or harp string, or harpsichord string, or violin string, even though all these strings are doing essentially the same thing when sounding the same note.